As with other posts in this series, this is the results of a test I took today, July 31st, 2021.
訳 口 働 冷 親 戻 専 届 的 雲 必 門 預 要 好 寝 港 勤 実 雷 僕 林 線 回 二 始
I only got two wrong in this test, one of the better scores in recent memory. This is likely due to the random choice of lower row kanji -- intended to force my brain to remember all 421 kanji I've learned. But in this test, the kanji that are from row 1-25 are: 口 冷 親 届 好 港 実 林 回 二. The rows these are from are 4, 16, 9, 23, 13, 21, 16, 8, 18, 1. Which ones did I get wrong? Row 23 and row 21. Note how I stopped my retesting at row 15 because I got such a bad score on it. Specifically I missed a stroke on 冷 but I got most of it. I looked at the banner in my room that has two penguins and that kanji drawn: 冷月中 to get the ice radical on the left. I don't consider that cheating because in a pinch I'll be able to draw it correctly. I forgot 届. This kanji was in KARAKARA, so I think about it when I see deliver, but I didn't think of door 戸 and rice paddy 田, which I should have. I forgot the reading of 要 but that's okay for now. I wrote the backwards 5 radical 已 in the lower right of 港. I am happy that my brain remembers 港 as a backwards 5. If we look at k_rads1.txt (a list of popular radicals for each kanji in my list) we find that 已 is found in 配, 起, and 港 so far.
What have I been up to instead of learning kanji? I've been playing a lot of games. Not the ones I should, but that's part of my gaming, getting away from stuff I'm supposed to do. If I spend all my time playing the games I'm supposed to, I'll overflow. Yesterday I mostly completed a task I gave myself May 25th, 2021. Not bad. It's reversibility of the function f(x) = ((x + 1) & 7) ^ ((x & 0xfffff8) - 4) which can be seen below in figure 1. Click the image to get a larger version. If you're a cryptographer, you might recognize this construction. It's hash-related. As you can see, this is a poorly-written hash for a specific reason. Why? It seems that the reversibility of functions relies upon a bit of stuff that seems pretty easy to produce, until you protect something with it. Mixing and obfuscation isn't enough. Symmetric ciphers rely on the fact that knowing a lot of the plaintext won't give you the key. Reversibility of a ciphertext to a key would be a cryptanalysis of a cipher assuming the ciphertext necessary to learn the key is substantially cheaper to obtain than brute force search of the key.
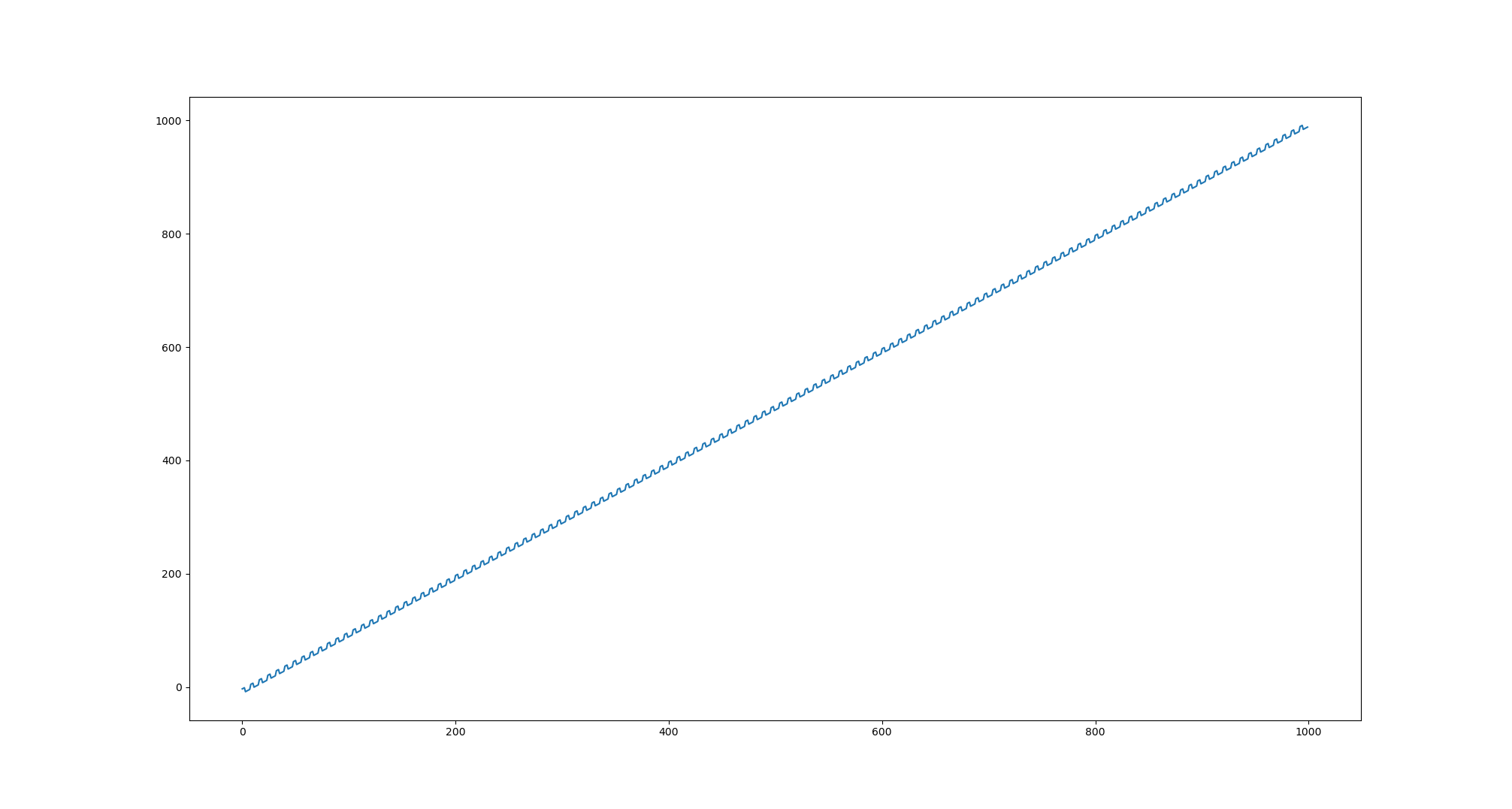
Figure 1: f(x) = ((x + 1) & 7) ^ ((x & 0xfffff8) - 4)
Until next time!
I'll hopefully post all tests as I pass them. Wish me 運.
Previous episodes:
Learning to Read and Write Kanji
Learning to Read and Write Kanji Row 5
Learning to Read and Write Kanji Row 6
Learning to Read and Write Kanji Row 7
Learning to Read and Write Kanji Row 8
Learning to Read and Write Kanji Row 9
Learning to Read and Write Kanji Row 10
Learning to Read and Write Kanji Row 11
Learning to Read and Write Kanji Row 12
Learning to Read and Write Kanji Row 13
Learning to Read and Write Kanji Row 14
Learning to Read and Write Kanji Row 15
Learning to Read and Write Kanji Row 16
Learning to Read and Write Kanji Row 17
Learning to Read and Write Kanji Row 18
Learning to Read and Write Kanji Row 19
Learning to Read and Write Kanji Row 20
Learning to Read and Write Kanji Row 21
Learning to Read and Write Kanji Row 22
Learning to Read and Write Kanji Row 23
Learning to Read and Write Kanji Row 24
Learning to Read and Write Kanji Row 25
Javantea out.
Permalink-
Leave a Reply






Comments: 0
Leave a reply »